The calculator allows you to expand and collapse an expression online , to achieve this, the calculator combines the functions collapse and expand For example it is possible to expand and reduce the expression following ( 3 x 1) ( 2 x 4), The calculator will returns the expression in two forms expanded and reduced expression 4 14 ⋅ x2 (x y) = 4 – 3y (c) 3 men and 4 boys can do a piece of work in 14 days, while 4 men and 6 boys can do it in 10 days Hence the value of (y 3 (1/y) 3) is 18 After having gone through the stuff given above, we hope that the students would have understood, " Using the Formula of Expansion of Binomial of Power 3" Apart from the stuff given in this section , if you need any other stuff in math, please use our google custom search here
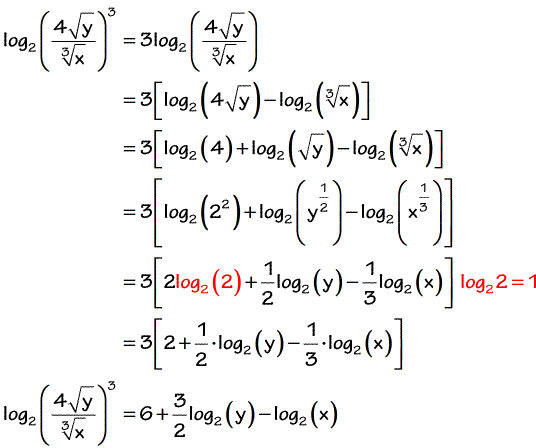
Expanding Logarithms Chilimath
(x-y)^3 expand formula
(x-y)^3 expand formula-The formula for (X – Y) whole cube, ie (X – Y) 3 is given by (X – Y) 3 = X 3 – Y 3 – 3XY(X – Y) Or (X – Y) 3 = X 3 – Y 3 – 3X 2 Y 3XY 2Learn about expand using our free math solver with stepbystep solutions Microsoft Math Solver Solve Practice Download Linear Equations Quadratic Equations Inequalities Systems of Equations Matrices (x3)(4x4) 3 (x
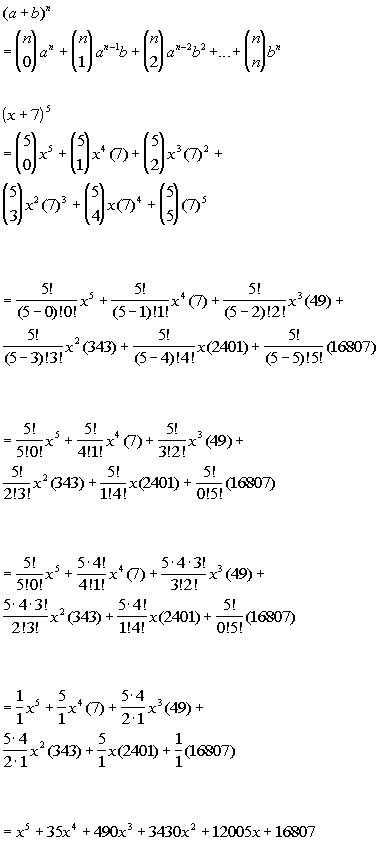



Tutorial 54 The Binomial Theorem
(b) Solve the following system of simultaneous linear equations by elimination method 9 – (x – 4) = y 7; Expand/collapse global hierarchy Home Bookshelves Calculus Supplemental Modules (Calculus) (P_3(x,y)\) and use this new formula to calculate the thirddegree Taylor polynomial for one of the functions in Example \(\PageIndex{1}\) aboveSuppose we have two cubes Let the volume of the first cube be x3and the volume of second cube y3 Let's join the cube side by side So, the total volume of the two cubes is, We already have an identity for (xy)3 So, let's try to derive the identity x3y3using the identity for (xy)3
Examples on (a b)^3 Formula Example 1 Solve the following expression using (a b) 3 formula (2x 3y) 3 Solution To find (2x 3y) 3 Using (a b) 3 Formula, (a b) 3 = a 3 3a 2 b 3ab 2 b 3 = (2x) 3 3 × (2x) 2 × 3y 3 × (2x) × (3y) 2 (3y) 3 = 8x 3 36x 2 y 54xy 2 27y 3 Answer (2x 3y) 3 = 8x 3 36x 2 y 54xy 2 27y 3 Example 2 Find the value of x 3 y 3 ifHow do you expand an equation into general form such as y=2 (x3)^28 y=2 (x3)^28 (1) (y8) = 2 (x3)^2 Squaring both the sides (y8)^2 = 2 (x3)^2^2 y^216y64 = 2^2 (x3)^2^2 (using (ab)^2 = a^2 2abb^2 formula on the LHS where a = y and b = 8)Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank you
Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Pi (Product) Notation Induction Logical Sets expand (xy)^3 en Related Symbolab blog posts My Notebook, the Symbolab wayThe first factor of the product is a sum containing 2 terms The first term of the sum is equal to X The second term of the sum is equal to Y The second factor of the product is equal to a sum consisting of 2 terms The first term of the sum is equal to X The second term of the sum is equal to negative Y open bracket X plus Y close bracket multiplied by open parenthesis X plus negative YLovely, expansion of binomials, first explored waybackwhen by Blaise Pascal (Ever heard of pascal's triangle?
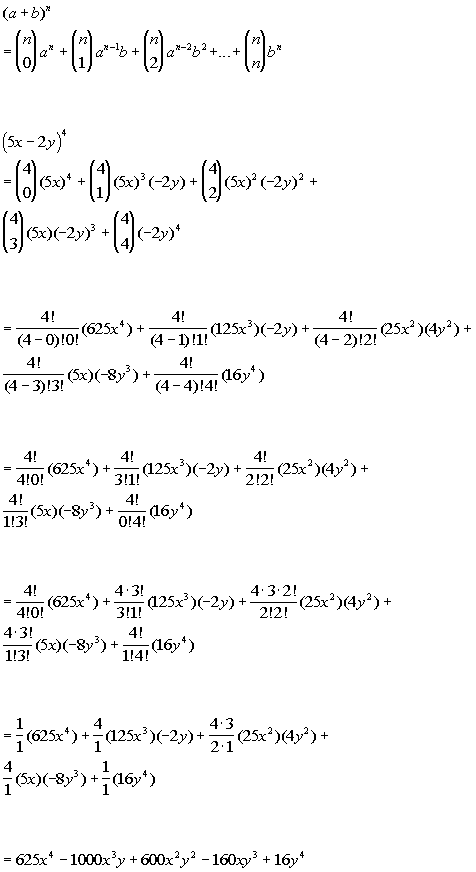



Tutorial 54 The Binomial Theorem




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
Trigonometry Expand (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x y 2 y 3Free expand & simplify calculator Expand and simplify equations stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more expand\(x^23y)^3;(x3f xxx3x 2yf xxy3xy 2f xyyy 3f yyy)··1 n!




Section 8 5 The Binomial Theorem Ppt Download
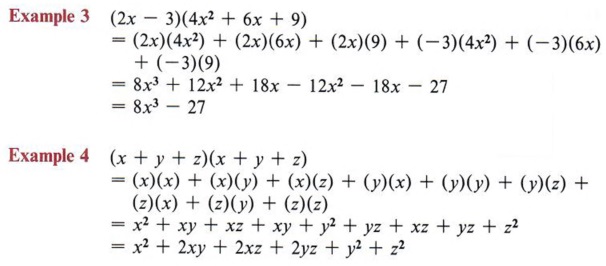



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver
1 Inform you about time table of exam 2 Inform you about new question papers 3 New video tutorials informationIntroduction x y is a binomial in which x and y are two terms In mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms ( x y) 3 = x 3 y 3 3 x 2 y 3 x y 2The Binomial Theorem – HMC Calculus Tutorial We know that ( x y) 0 = 1 ( x y) 1 = x y ( x y) 2 = x 2 2 x y y 2 and we can easily expand ( x y) 3 = x 3 3 x 2 y 3 x y 2 y 3 For higher powers, the expansion gets very tedious by hand!




Properties Of Logarithms Algebra Ii Quiz Quizizz




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9
Expandcalculator en Related Symbolab blog posts Middle School Math Solutions – Equation CalculatorWhy create a profile on Shaalaacom?Answer (1 of 4) (xyz)^3 put xy = a (az)^3= a^3 z^3 3az ( az) = (xy)^3 z^3 3 a^2 z 3a z^2 = x^3y^3 z^3 3 x^2 y 3 x y^2 3(xy)^2 z 3(xy) z^2 =x^3 y^3 z^3 3 x^2y 3xy^2 3 ( x^2 y^2 2xy ) z 3x z^2 3yz^2 =x^3y^3z^3 3x^2 y3xy^2 3x^2 z 3y^2 z 6xyz 3xz^2 3



1




Table 1 From Generalized Ismail S Argument And F G Expansion Formula Semantic Scholar
You can put this solution on YOUR website!X^3 y^3 z^3 3x^2y 3xy^2 3x^2z 3z^2x 3y^2z 3z^2y 6xyz Lennox Obuong Algebra Student Email obuong3@aolcom(a 3 3a 2 b 3ab 2 b 3)(ab) = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4 The calculations get longer and longer as we go, but there is some kind of pattern developing That pattern is summed up by the Binomial Theorem




Working With Symbolic Expressions Manning
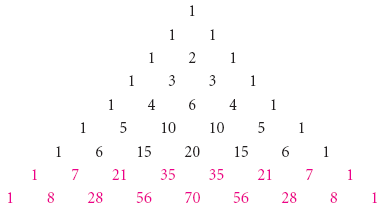



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
Key Takeaways Key Points According to the theorem, it is possible to expand the power latex(x y)^n/latex into a sum involving terms of the form latexax^by^c/latex, where the exponents latexb/latex and latexc/latex are nonnegative integers with latexbc=n/latex, and the coefficient latexa/latex of each term is a specific positive integer depending on latexn/latex= 1 ⋅ 2 ⋅ ⋅ n We have that a = 2 x, b = 5, and n = 3 Therefore, ( 2 x 5) 3 = ∑ k = 0 3 ( 3 k) ( 2 x) 3 − k 5 k Now, calculate the product for every value of k from 0 to 3 Thus, ( 2Theorem Taylor's Formula for f(x,y) at the Origin Suppose f(x,y) and its partial derivatives through order n 1 are continuous throughout an open rectangular region R centered at the point (0,0) then throughout R, f(x,y) = f(0,0) xfx yfy 1 2!



Expand X Y Z Square Brainly In




Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo
Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)3) Solve the equation x 2 25 = 0 Solution x 2 25 = (x 5)(x 5) => we have to solve the following 2 equations x 5 = 0 or x 5 = 0 so the equation have two decisions x = 5 and x = 5 Related Resources Polynomial identities quiz Simplifying polynomial expressions problems with solutions Factoring polynomials problems withFind the product of two binomials Use the distributive property to multiply any two polynomials In the previous section you learned that the product A (2x y) expands to A (2x) A (y) Now consider the product (3x z) (2x y) Since (3x z) is in parentheses, we can treat it as a single factor and expand (3x z) (2x y) in the same




Expand Using Formula X Y 3 Brainly In



What Is The Expansion Of A B C 3 Quora
Identify binomial coefficients given the formula for a combination Expand a binomial using the binomial theorem Use the binomial to find a single term in a binomial Previously, we studied combinations In the shortcut to finding latex{\left(xy\right)}^{n}/latex, we will need to use combinations to find the coefficients that will appear(x y) 5 (x – y) 5 = 25C 0 x 5 5C 2 x 3 y 2 5C 4 xy 4 = 2(x 5 10 x 3 y 2 5xy 4) Now (√2 1) 5 (√2 − 1) 5 = 2(√2) 5 10(√2) 3 (1) 2 5(√2)(1) 4 =58√2 Binomial Expansion Important points to remember The total number of terms in the expansion of (xy) n are (n1) The sum of exponents of x and y is always n The algebraic formulas for the three variables a, b and c and a maximum degree of 3 can be quickly taken by multiplying the expression by itself, based on the exponent value of the algebraic expression You can see the basic algebraic formulas given below 1 (a b)2 = a2 2ab b2 2 (a– b)2 = a2– 2ab b2
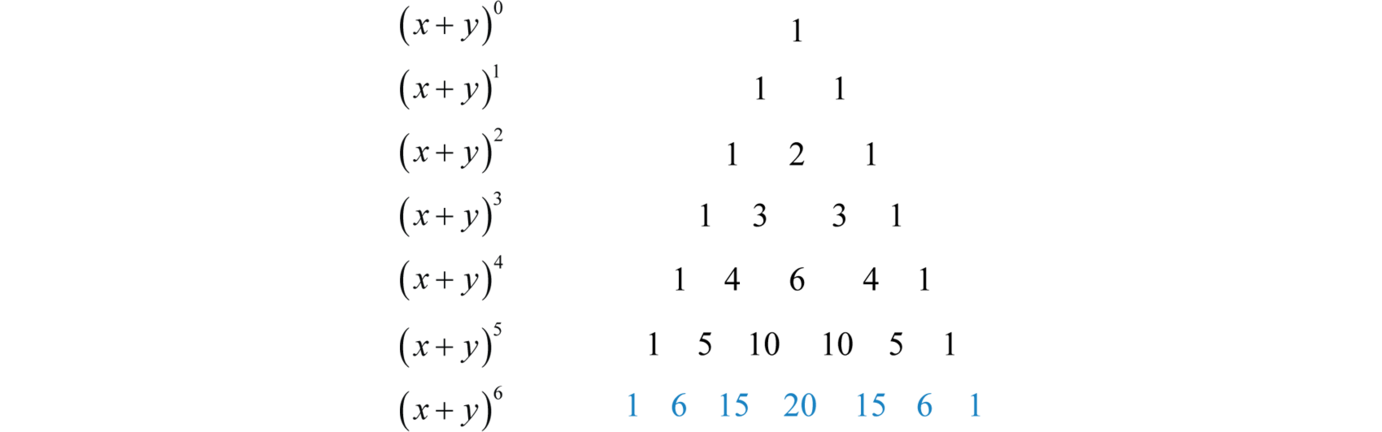



Binomial Theorem




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube
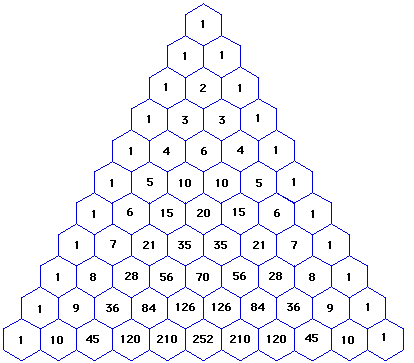
Summation of two cubes x 3 y 3 = (x y) (x 2 xy y 2) Cube of difference (x y) 3 = x 3 3x 2 y 3xy 2 y 3 Difference of two cubes x 3 y 3 = (x y) (x 2 xy y 2) © Copyright 00 21, by Engineers Edge, LLC wwwengineersedgecom All rights reserved Disclaimer #(xy)^3=(xy)(xy)(xy)# Expand the first two brackets #(xy)(xy)=x^2xyxyy^2# #rArr x^2y^22xy# Multiply the result by the last two brackets #(x^2y^22xy)(xy)=x^3x^2yxy^2y^32x^2y2xy^2# #rArr x^3y^33x^2y3xy^2#The primary example of the binomial theorem is the formula for the square of xy The coefficients 1, 2, 1 that appear in this expansion are parallel to the 2nd row of Pascal's triangle (Because the top "1" of the triangle is row 0) The coefficients of higher powers of x y on the other hand correspond to the triangle's lower rows
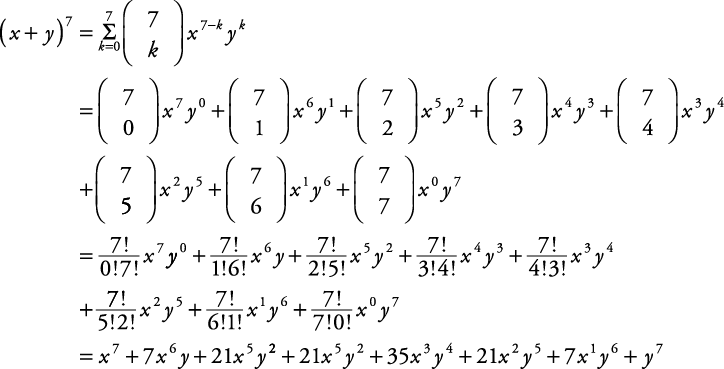



Binomial Coefficients And The Binomial Theorem



1
243x 5 810x 4 y 1080x 3 y 2 7x 2 y 3 240xy 4 32y 5 Finding the k th term Find the 9th term in the expansion of (x2y) 13 Since we start counting with 0, the 9th term is actually going to be when k=8 That is, the power on the x will 138=5 and the power on the 2y will be 84 Binomial Expansions 41 Pascal's riTangle The expansion of (ax)2 is (ax)2 = a2 2axx2 Hence, (ax)3 = (ax)(ax)2 = (ax)(a2 2axx2) = a3 (12)a 2x(21)ax x 3= a3 3a2x3ax2 x urther,F (ax)4 = (ax)(ax)4 = (ax)(a3 3a2x3ax2 x3) = a4 (13)a3x(33)a2x2 (31)ax3 x4 = a4 4a3x6a2x2 4ax3 x4 In general we see that the coe cients of (a x)nThe calculator can also make logarithmic expansions of formula of the form `ln(a^b)` by giving the results in exact form thus to expand `ln(x^3)`, enter expand_log(`ln(x^3)`), after calculation, the result is returned The calculator makes it possible to obtain the logarithmic expansion




Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange




Expanding Algebraic Expressions Using Identities Worksheets
The question that I have to solve is an answer on the question "How many terms are in the expansion?" Depending on how you define "term" you can become two different formulas to calculate the terms in the expansion of $(xyz)^n$ Working with binomial coefficients I found that the general relation is $\binom{n2}{n}$And E(X1)5 = 55 = 25 V(X1 X2 X3) = V(X1) V(X2) V(X3) = 25 25 25 = 75 Rule 16 If X and Y are independent, V(X ±This calculator can be used to expand and simplify any polynomial expression




Binomial Theorem Wikipedia




Factorise X 5 Y 5
( n − k)!In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial According to the theorem, it is possible to expand the polynomial n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive integer depending on n and b For example, 4 = x 4 4 x 3 y 6 x 2 y 2 4 x y 3 y 4 {\displaystyle ^{4}=x^{4}4x^{3}y6x^{2}y^{2}4xy^{3}yIf a binomial expression (x y) n is to be expanded, a binomial expansion formula can be used to express this in terms of the simpler expressions of the form ax by c in which 'b' and 'c' are non negative integers The value of 'a' completely depends on the value of 'n' and 'b'
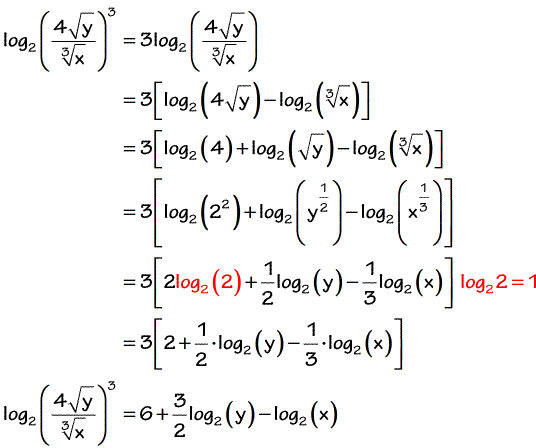



Expanding Logarithms Chilimath




The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
Great simple way to expand and simplify polynomials) Pascal's triangle says that the coefficients of (xy)^x form a pattern in the shaFortunately, the Binomial Theorem gives us the expansion for any positive integer powerRule 8 E(X Y) = E(X) E(Y), ie Expectation of a sum = Sum of the Expectations V(X1) = V(X2) = V(X3) = E(X15) E(X1)5 = 5 25 = 25 Rule 3 Definition of the variance Since X15 = X1, E(X15) = E(X1) = 5;




Expanding Binomials Video Series Khan Academy




Taylor S Series Expansion An Overview Sciencedirect Topics
All Steps Visible Step 1 Third term Step 1 Answer $$a_ {3} =\left (\frac {5!} {2!3!} \right)\left (a^ {3} \right)\left (\sqrt {2} \right)^ {2} $$ Step 2 Expand the coefficient Step 2 Answer $$a_ {3} =\left (\frac {4\times 5\times 3!} {2\times 3!} \right)\left (a^ {3} \right)\left (\sqrt {2} \right)^ {2} $$ x^33x^23x1 "note that" (xa)^3=x^3(aaa)x^2(aaaaaa)xa^3 (x1)^3toa=1 rArr(x1)^3=x^3(111)x^2(111)x(1)^3 =x^33x^23x1 \ f(x,y,z) = x^2 \cos (xz) 2 \, \sin^2 (xyz) (xzy)^3 Simplify the expression in the following ways a) define a new function g(x,y) such that \( z = 2 ;
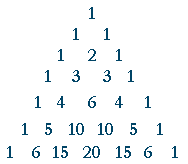



Binomial Theorem Topics In Precalculus




Learn Algebraic Identities Of X Y And X Y In 3 Minutes
Circle on a Graph Let us put a circle of radius 5 on a graph Now let's work out exactly where all the points are We make a rightangled triangle And then use Pythagoras x 2 y 2 = 5 2 There are an infinite number of those points, here are some examples👉 Learn all about sequences In this playlist, we will explore how to write the rule for a sequence, determine the nth term, determine the first 5 terms orSo to find the expansion of (x − y) 3, we can replace y with (− y) in (x y) 3 = x 2 3 x 2 y 3 x y 2 y 3 This is the required expansion for ( x − y ) 3 Let's now use these identities to




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange
(x2f xx 2xyfxy y2fyy) 1 3!An outline of Isaac Newton's original discovery of the generalized binomial theorem Many thanks to Rob Thomasson, Skip Franklin, and Jay Gittings for theirSolution The expansion is given by the following formula ( a b) n = ∑ k = 0 n ( n k) a n − k b k, where ( n k) = n!




Solved Expand 1x Y3 3 Maths Questions



Factorials To Binomial Theorem
Two numbers r and s sum up to 8 exactly when the average of the two numbers is \frac{1}{2}*8 = 4 You can also see that the midpoint of r and s corresponds to the axis of symmetry of the parabola represented by the quadratic equation y=x^2BxC compared with ( 2 x − x 2) 6 we can use the substitution y = x − x 2 and the result is (2) ( 2 x − x 2) 2 = 64 192 ( x − x 2) 240 ( x − x 2) 2 160 ( x − x 2) 3 ⋯ Since we only need an expansion with powers up to x 3 we don't need any terms ( x − x 2) n with n > 3 We also recall the binomial formulas ( a b) n




Differential Equations Linear Algebra Only People That Are Proficient In Differential Equations Should Even Attempt Homeworklib




Question About Book Solution To Estimate E E Xy When X And Y Are Independent Exponential Rvs With Lambda 1 Mathematics Stack Exchange



A Lesson In Making Use Of Structure From With Jmccalla1 Experiments In Learning By Doing



Is There A Shortcut To Expand The Equation X Y Quora




8 5 The Binomial Theorem Warm Up Copyright C By Houghton Mifflin Company Inc All Rights Reserved 2 X Y 3 X 3 3x 2 Y 3xy 2 Y Ppt Download
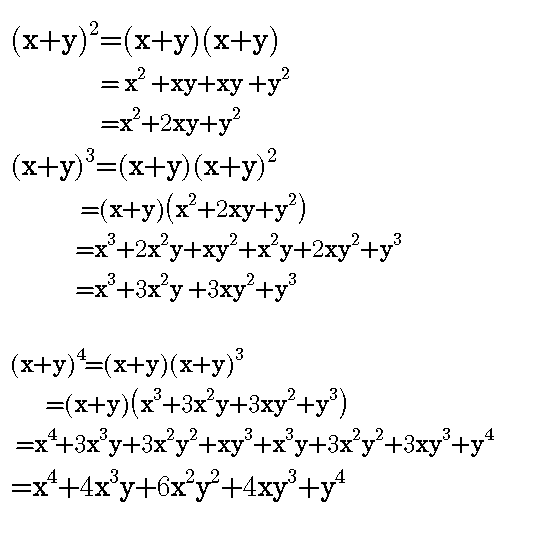



Worked Examples On Binomial Expansion Steemit




9 Binomial Theorem Example 4 Expanding 3 Terms In A Binomial Question Youtube



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver




2 6 Some Useful Orthogonal Functions Orthogonal Wx
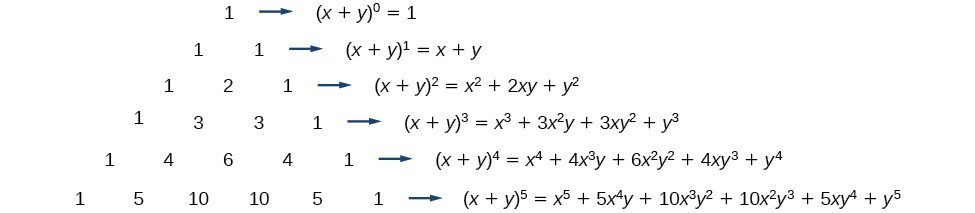



Using The Binomial Theorem College Algebra
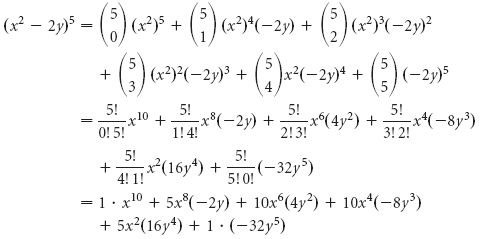



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets




Using Laws Of Logarithms Laws Of Logs To Solve Log Problems Krista King Math Online Math Tutor




X 3 Y 3 X 3 Y 3 Formula Proof Youtube




Expanding Logarithms




How Can We Expand X Y 1 2 Youtube
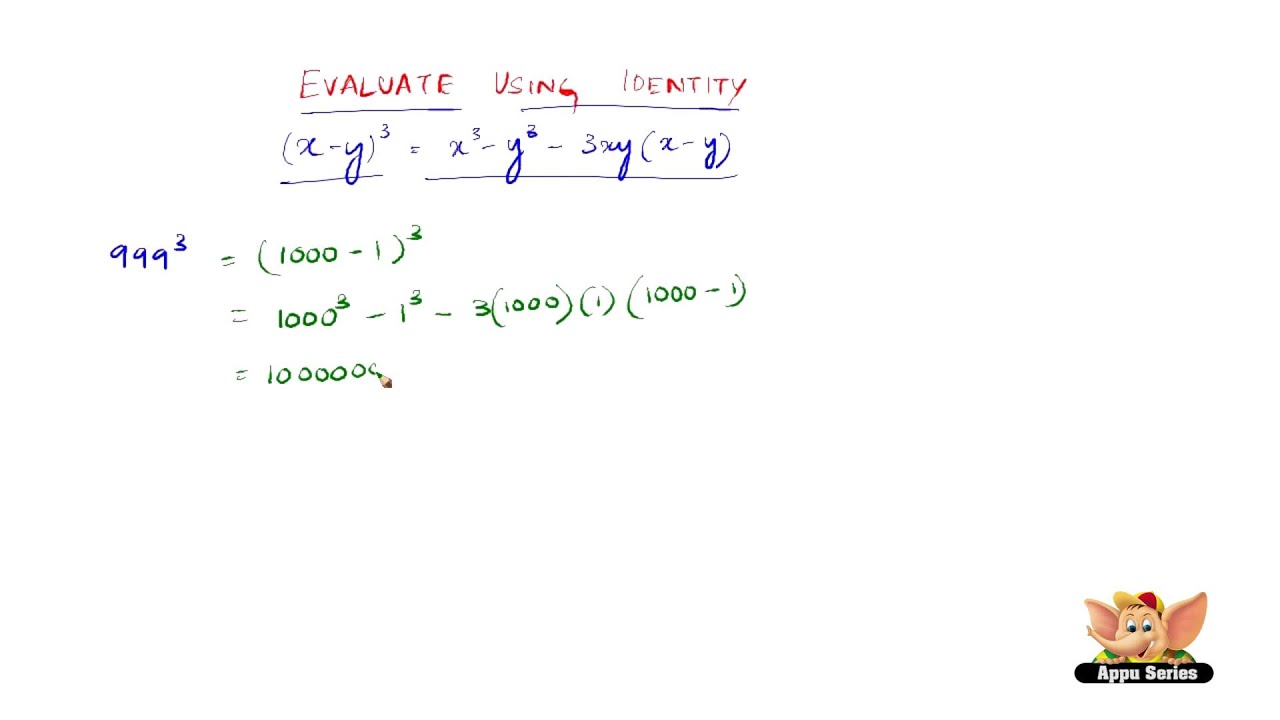



How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx By Appuseriesacademy




Cot A B Formula Cot X Y Identity




Binomial Theorem Protonstalk




How Do You Expand X Y 6 Using Pascal S Triangle Socratic
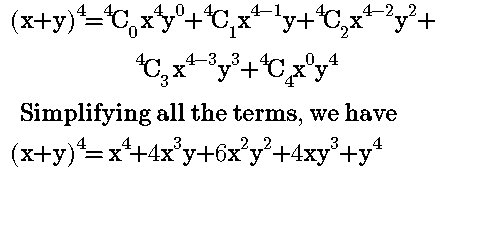



Worked Examples On Binomial Expansion Steemit




A Quick And Efficient Way To Expand Binomials Ppt Download



4 The Binomial Theorem



What Is The Answer Of X Y Quora
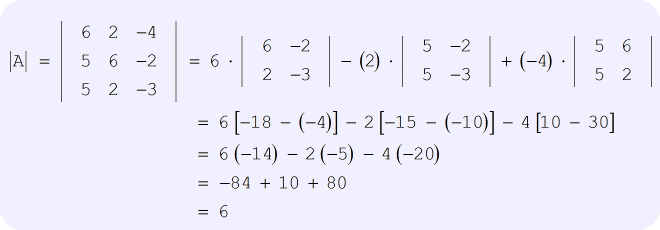



Cramer S Rule With Three Variables Chilimath
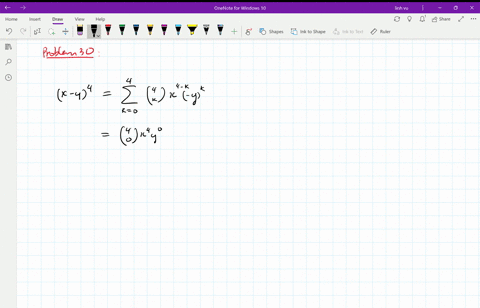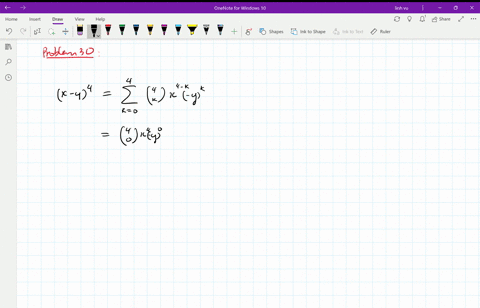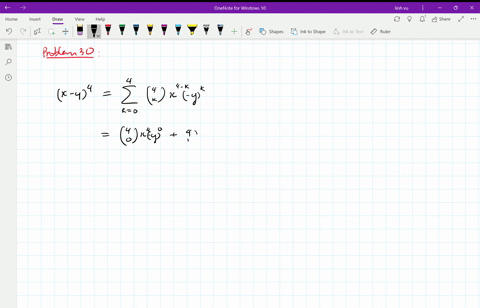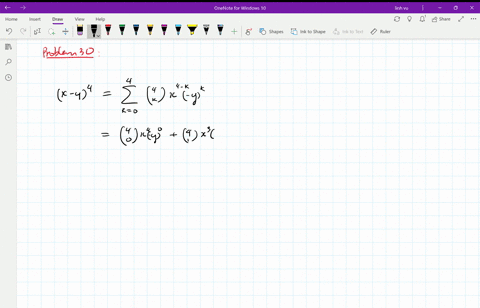



Solved Find The Expansion Of X Y 4 A Using Combinatorial Reasoning As In Example 1 B Using The Binomial Theorem




Expand And Simplify Binomial Squares 2x 3y 2 Youtube




Polynomial Expansion And Pascal S Triangle Ck 12 Foundation
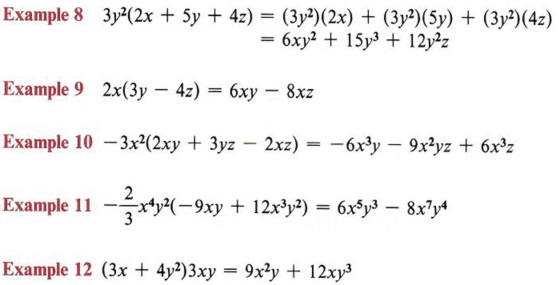



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver




Exponent Rules 7 Key Strategies To Solve Tough Equations Prodigy Education




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf




The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium




A B N And A B N Formula Expander




Sec 9 3 Conic Sections Parabola




Find The Coefficient Of X 6y 3in The Expansion Of X 2y 9




How Do You Expand The Binomial X Y 5 Socratic



How To Factor X Y 3 8 X Y 3 Quora
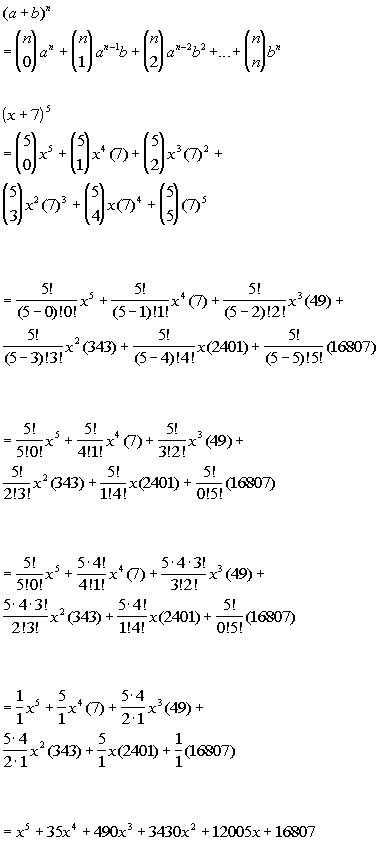



Tutorial 54 The Binomial Theorem




Using The Binomial Theorem College Algebra




9 5 The Binomial Theorem Let S Look At The Expansion Of X Y N Ppt Video Online Download




Binomial Theorem Wikipedia Republished Wiki 2



How Do You Expand X Y 10 Socratic




Conic Section From Expanded Equation Ellipse Video Khan Academy




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



Expanding Polynomial Factors Maths First Institute Of Fundamental Sciences Massey University




Ex 2 5 6 Write The Following Cubes In Expanded Form I 2x 1 3



2 Use The Rules Of Logs To Expand Each Of The Chegg Com




8 5 The Binomial Theorem Mathematics Libretexts




Baker Campbell Hausdorff Formula Wikipedia
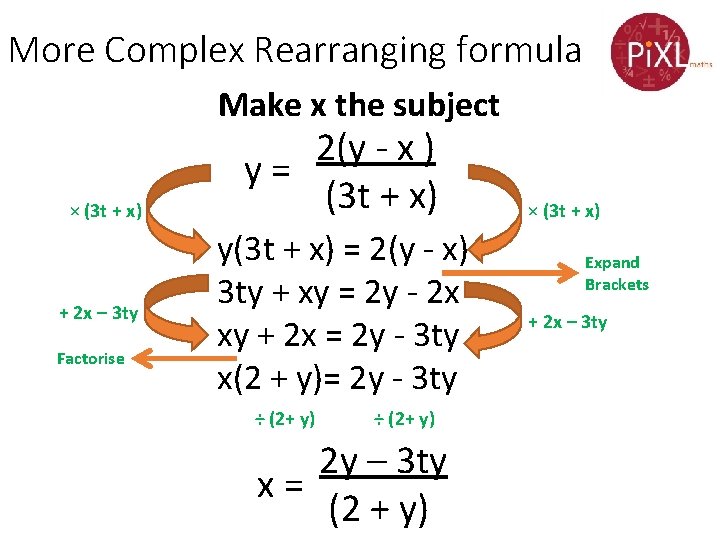



Grade De Changing The Subject Change The Subject




The Binomial Theorem Defining Expressions Video Lesson Transcript Study Com




How Do You Use The Binomial Theorem To Expand X Y 5 Socratic



1



How To Expand The Binomial X Y 10 Quora




Question 2 46 Marks 2 1 Expand And Simplify The Chegg Com
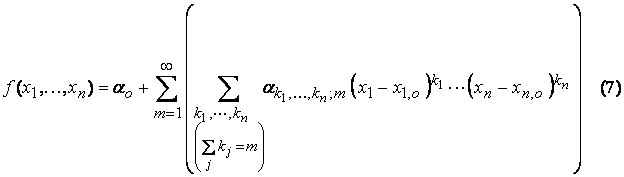



Taylor Series Expansion




Problem 3 10 Points Consider The Ode Y Xy 2y Chegg Com
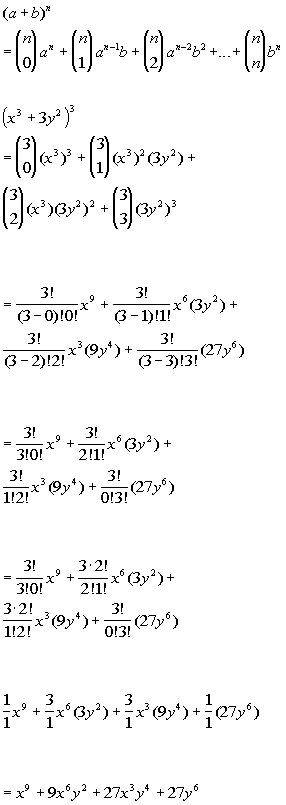



Tutorial 54 The Binomial Theorem




9 9 Pts A State The Binomial Theorem B Find Chegg Com
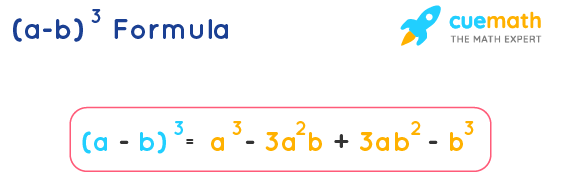



A Minus B Whole Cube Formula Examples A B 3 Formula




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Using The Binomial Theorem College Algebra
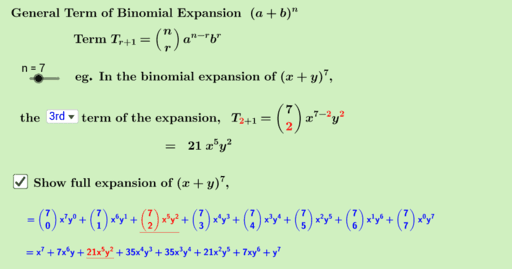



General Term Of Binomial Expansion Geogebra




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf




3 The Formula For The Taylor Expansion Of The Second Chegg Com




Binomial Expansion Formulas Derivation Examples




Section 8 5 The Binomial Theorem Ppt Download




Expand X Y 3 Solved




Expand Each Of The Following I X 2 Y 3 2 Ii X 5 X 3



Factorials To Binomial Theorem



Is There A Shortcut To Expand The Equation X Y Quora



No comments:
Post a Comment