Let us use elimination method to solve the given system of equations Multiply (2) by 3 And subtract both the equations From (1); by cross multiplication x/b1c2b2c1=y/a2c1a1c2 =1/a1b2a2b1 x/1331=y/3432 =1/2141 x/33=y/126=1/24 X/6=Y/6=1/6 X/6=1/6 Y/6=1/6 X=1 AND Y=1 HENCE SOLVEDSolving equations with fractions cross multiplication – worksheet 5 Alternative versions feel free to create and share an alternate version that worked well for your class following the guidance here
Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community
X-y=3 x/3 y/2=6 by cross multiplication method
X-y=3 x/3 y/2=6 by cross multiplication method-Math, 0210, vaibhavKhatri Solve the following equation by Cross multiplication method 2/x3/y=17; Cross multiplication – PowerPoint;




How To Solve Equations With Three Variables By Cross Multiplication Method Quora
Solve by Graphing xy=5 , xy=3, Subtract from both sides of the equation Subtract from both sides of the equation Multiply each term in by Tap for more steps Multiply each term in by Multiply Tap for more steps Multiply by Multiply by Simplify each term Tap for more steps Multiply by Multiply Tap for more stepsAnswer to Solve 3 x 4 y = 10 and 4 x 3 y = 5 by the method of cross multiplication By signing up, you'll get thousands of stepbystepIndirect proportion — »the more, the less« If the car is driven at an average speed of 70 km/h, it will take 40 minutes
Which of the following pair of linear equations has unique solution, no solution or infinitely many solutions In case there is a unique solution, find it by using cross multiplication method 2 x y = 5 3 x 2 y = 8We can use cross multiplication method As And get value of x and y As Here a 1 = 2 , b 1 = 3 And c 1 = 9 And a 2 = 3 , b 2 = 7 And c 2 = 2 So, x = 3 × 2 7 × 9 2 × 7 3 × 3 ⇒ x = 6 63 14 9 ⇒ x = 69 23 ⇒ x = 3 ( Ans ) And Transcript Example 17 Solve the pair of equations 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 So, our equations become 2u 3v = 13 5u – 4v = –2 Hence, our equations are 2u 3v = 13 (3) 5u – 4v = – 2
I'll answer by the elimination method x2/3 y1/6 = 2 x3/4 2y1/2 = 1 6x 4 6y 1 = 12 (multiplying both sides by 6) 4x 3 8y 2 = 4 (multiplying both sides by 4) 6x 6y = 15 4x 8y = 3 (4)(6x 6y = 15) (multiplying both sides by 4Class 10 Maths Linear Equations in 2 Variables Cross Multiplication Method Cross Multiplication Method Let's assume that we have to find solution for a 1 x b 1 y c 1 = 0 (i) and a 2 x b 2 y c 2 = 0 (ii) Step 1 Multiply Equation (i) by b 2 and Equation (ii) by b 1, to get b 2 a 1 x b 2 b 1 y b 2 c 1 = 0 (iii) Solve, using crossmultiplication 3x 4y = 11 2x 3y = 8 Answer Given equations are 3x 4y = 11 and 2x 3y = 8 Comparing with a 1 x b 1 y c 1 = 0 and a 2 x b 2 y c 2 = 0, we have a 1 = 3, b 1 = 4, c 1 = 11 and a 2 = 2, b 2 = 3, c 2 = – 8 Question 3 Solve, using crossmultiplication 6x 7y – 11 = 0 5x 2y = 13 Answer




How To Solve Equations With Three Variables By Cross Multiplication Method Quora



Method Of Cross Multiplication Solve By Method Of Cross Multiplication
Chapter 3 Ex36 Question 1 Solve the following pairs of equations by reducing them to a pair of linear equations (i) 1 2x 1 3y = 2 1 3x 1 2y = 13 6 1 2x 1 3y = 2 1 3x 1 2y = 13 6 (ii) 2 √x 3 √y = 2 4 √x − 9 √y = − 1 2 √x 3 √y =2 4 √x − 9 √y =−1 (iii) 4Given system is (1/x) (1/y) = 7 (1) (2/x) (3/y) = 17 (2) For doing it by cross multiplication method there's an easy pattrern , by whichContents1 Solving Linear Equations by CrossMultiplication method Example12 Solving Linear Equations by CrossMultiplication method Example23 Solving Linear Equations by CrossMultiplication method Example34 Solving Linear Equations by CrossMultiplication method Example4 Consider the equation Clearly, it is an equation of the form , where a = 2, b = 5, c =




Solve The Following System Of Equations By Method Of Cross Mult



Mfm2p
Xy=3 x/3y/2=6 by cross multiplication method Utkarsh171 is waiting for your help Add your answer and earn pointsAlgebraic methods Systems of equations with substitution 3x4y=2 & y=2x5 Practice Systems of equations with substitution Systems of equations with elimination (and manipulation) Practice Systems of equations with elimination Practice Systems of equations with elimination challenge Practice Solving system of equations through crossSolve the Following Pairs of Linear (Simultaneous) Equation Using Method of Elimination by SubstitutionX/6 Y/15 = 4 X/3 Y/12 = 4 3/4 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 5 Question Bank Solutions Concept Notes




Which Of The Following Pairs Of Linear Equations Has Unique Solution No Solution Or Infinitely Many Solutions I X 3y 3 0 3x 9y 2 0




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube
Multiplying equation (1) by ab, we get bx ay – ab (a b) = 0 (3) Multiplying equation (2) by a 2 b 2, we get b 2 x a 2 y – 2a 2 b 2 = 0 (4) Using formula for cross multiplication method So, from equation (1) and (2) we can write the value of a,b and c Hence, the solution x = a 2, y = b 2 The pair of linear equations can be written using cross multiplication method as, x y 1 – 2b a 4b 2a – 2bExample 2 Solve the equation x 3 = 10 6 1 Cross multiply the denominator of one with the numerator of the other obtain the equation 6 × x = 3 × 10 2 Divide both sides by the coefficient of x which is 6 6 × x 6 = 3 × 10 6 3 Simplify to find x x = 5 It can be used to verify if two fractions are equivalent




X Y 6 X Y 2 By Elimination Method Novocom Top




How To Solve Equations With Three Variables By Cross Multiplication Method Quora
Graph{x^33x^29x5 1459, 1726, 856, 736} FIrst determine the interval of definition, then the behavior of first and second derivatives and the behavior of CrossMultiplication Method This method looks more complex than the other methods, but it is one of the most efficient ways to solve linear equations Let's say the two lines whose equation is, a 1 x b 1 y c 1 = 0 a 2 x b 2 y c 2 = 0 In this crossmultiplication method, The solution is given by,Xy=3 2xy=_2 by cross multiplication method fatimazahra54 fatimazahra54 Math Secondary School answered Xy=3 2xy=_2 by cross multiplication method 2 See answers srijitachakravorty srijitachakravorty




Solve The Following System Of Equation 2x 3y 8 0 4x 5y 14 0




X 2 2y 3 1 X Y 3 3 Solve The Given Equation Using Elimination And Substitution Method Youtube
x = 3 y = 2 Stepbystep explanation x 2y 1 = 0 2x 3y 12 = 0 Multiply first equation by 22x 4y 2 = 0 2x 3y 12 = 0 Add equations 0x 7y 14 = 0 Solve for y7y = 14 y =2 Put y as 2 in the first equation and solve for x x2(2)1=0 x 4 1 = 0 x = 0 4 1 x = 3Solve the following pair of linear equations by the substitution and crossmultiplication methods 8x 5y = 9, 3x 2y = 4 SOLUTION Soln Method1 Substitution method Thus, x = 2 and y = 5 Method 2 Cross Multiplication Method For 8x 5y 9 = 0, 3x 2y 4 = 0 By cross multiplication, we have ⇒ x = 1 × 2 = 2 and y = 1 × 5 = 5Solve for x Use the distributive property to multiply xy by x^ {2}xyy^ {2} and combine like terms Use the distributive property to multiply x y by x 2 − x y y 2 and combine like terms Subtract x^ {3} from both sides Subtract x 3 from both sides Combine x^ {3} and x^ {3} to get 0 Combine x 3 and − x 3 to get 0




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4




G 1 Coaching Class 3rd Chapter Pair Of Linear Equation In Two Variable
By using cross multiplication, we get 6 7 − 1 1 5 2 − 1 3 7 × (− 1 3) − 2 × (− 1 1) x = − 1 1 × 5 − (− 1 3) × 6 y = 6 × 2 − 7 × 5 1 − 9 1 2 2 x = − 5 5 7 8 y = 1 2 − 3 5 1 − 6 9 x = 2 3 y = − 2 3 1 x = 3, y = − 1 Hence, the value of x and y is 3, − 1Crossmultiplication Crossmultiplication is a procedure for calculating direct and indirect proportion Direct proportion — »the more, the more« 1 brick weighs 5 kg, how much do 150 bricks weight? Ex 35, 3 (Substitution method) Solve the following pair of linear equations by the substitution and crossmultiplication methods 8x 5y = 9 3x 2y = 4 8x 5y = 9 3x 2y = 4 From (1) 8x 5y = 9 8x = 9 – 5y x = ((9 − 5𝑦))/8 Putting value of x in (2) 3x 2y = 4 3 (((9



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community




Ncert Class 10 Chapter 3 Pair Of Linear Equations In Two Variables
In case there is a unique solution, find it by using cross multiplication method (i) x – 3y – 3 = 0 and 3x – 9y – 2 = 0 (ii) 2x y = 5 and 3x 2y = 8 Solve(cross multiplication method) 2/x3/y=2 1/x1/2y=1/3 Share with your friends Share 16 Dear student T a k i n g 1 x = u a n d 1 yCROSS MULTIPLICATION METHOD This is one of the methods we use to solve system of linear equations Let us consider the following system of linear equations a 1 x b 1 y c 1 = 0 a 2 x b 2 y c 2 = 0 We have to write the coefficients of the equations and do cross multiplication as shown below We write the coefficient of y and constant




Rd Sharma Solutions For Class 10 Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 4 Avail Pdf




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4
Hence the solution is (3, 1) (iii) (2/x) (3/y) = 5, (3/x) (1/y) 9 = 0 Solution Let 1/x = a and 1/y = b 2a 3b 5 = 0 (1) 3a b 9 = 0 (2) a/ (27 5) = b/ (15 18) = 1/ (2 9) a/ (22) = b/ (33) = 1/ (11) a = 22/ (11) = 2, b = 33/ (11) = 3Question 10 Solve the following equations by the method of crossmultiplication 2x 3y = 9 3x 4y = 5 Solution Given linear equations are 2x 3y = 9 3x 4y = 5 Comparing with the standard form, a 1 = 2, b 1 = 3, c 1 = 9 a 2 = 3, b 2 = 4, c 2 = 5 Using crossmultiplication method, x/(b 1 c 2 – b 2 c 1) = y/(c 1 a 2 – c 2 a 1) = 1/(a 1 b 2 – a 2 b 1)To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Solve by cross multiplication `x2y1=0 `, `2x3y12=0`



How Do You Solve The System Of Equations X Y 8 X Y 4 By Graphing Socratic




Ex 3 5 1 Which Pair Has Unique No Solution Or Infinitely
Let us eliminate y from the given equations The coefficients of y in the equations (iii) and (iv) are 3 and 2 respectively The LCM of 3 and 2 is 6 So, we make the coefficient of y equal to 6 in the two equations Multiplying (iii) by 2 and (iv) by 3, we get 8x 6y = 264 (v)The cross product is anticommutative Under this map, the cross product of 3vectors corresponds to the commutator of 3x3 skewsymmetric matrices Producing a single matrix by multiplying pair of matrices (may be 2D / 3D) is called as matrix multiplication which is the binary operation in mathematics In thisFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor




Solve The Following System Of Equation By Using Cross Multiplication Method 2x 5y 1 2x 3y 3 0



1
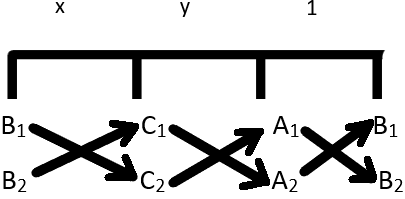
Cross multiply those constants Express the cross multiplicands of x, y, and constants under x, y, and 1 Equate them to find the values of x, y Check out the derivation to get more details about the CrossMultiplication Method General Solution Using the Method of CrossMultiplication Let the pair of linear equations in two variables areTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Solve `3xy2=0 , 2xy8=0` by method of cross multiplicationThis is the simplest method and gives the accurate value of the variables Cross multiplication is only applicable when we have a pair of linear equations in two variables Let us suppose that a 1 x b 1 y c 1 = 0 and a 2 x b 2 x c 2 = 0 are the two equations which has to be solved By using cross multiplication, we will get the values x and y such as



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions
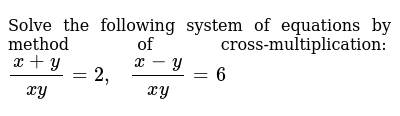



Solve The Following System Of Equations By Method Of Cross Mult
Solve each of the following systems of equations by the method of cross multiplication Question 15 2ax 3by = a 2b and 3ax 2by = 2a b Solution Given that, 2ax 3by = a 2b 3ax 2by = 2a b On comparing both the equation with the geneal form we get Solve this by cross multiplication method 2(ax by) a 4b = 0 2(bxay) b 4a = 0 For what values of a the following pair of equation 4x3y=3 and 8xay=5 will have a unique solution Without drawing graph, check whether the lines 3x y = 10 and 6x By cross – multiplication, we get x = 11 and y = 4 Try these questions now 1 Solve the following system of equations by using the method of cross multiplication 2x 3y = 17 3x 2y = 6 (Answer x = 4 and y = 3) 2 Solve the following system of equations by using the method of cross multiplication 2x y = 3 4x y = 3 (Answer x = 1



Systems Of Linear Equations




Solve The System Of Equation By The Method Of A Cross Multiplication 2x Y 6 X Y 2 Maths Pair Of Linear Equations In Two Variables Meritnation Com
9x – 2(9) = 108 x = 14 Answer x = 14 and y = 9TYPE/TOPIC OF QUESTIONS SOLVING EQUATIONS BY SUBSTITUTION, ELIMINATION, CROSSMULTIPLICATION, GRAPHICALLY 4 Solve the following simultaneous equations graphically (a) x 2y = 4 3x 5y = 1 (b) 4x 9y = 5 5x 3y = 8 5 Solve the following simultaneous equations by substitution method ⇒ 2/x 3/y = 5(ii) Putting 1/x = u and 1/y = v, we get 3u – v = 9 (iii) 2u 3v = 5 (iv) On multiplying (iii) by 3, we get 9u – 3v = 27 (v) On adding (iv) and (v), we get 11u = 22 ⇒ u = 2 ⇒ 1/x = 2 ⇒ x = −1/2 On substituting x = −1/2 in (i), we get



Solve Each Of The Following Systems Of Equations By The Method Of Cross Multiplication 2x Y 6 0 X Y 2 0 Sarthaks Econnect Largest Online Education Community




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15
Solving Linear Equations by Cross Multiplication Method Here is an example Suppose that we have to solve the following pair of equations 2x 3y−11 = 0 3x 2y−9 = 0 2 x 3 y − 11 = 0 3 x 2 y − 9 = 0 Our solution equality will be of the following form, where we have to figure out the question marksOn crossmultiplying 40 × 12 = 8 × x 480 ⁄ 8 = x 60 = x Therefore, the cost of 12 candle holders is $60 Fun Facts Crossmultiplication can be used to add or subtract unlike fractions quickly Crossmultiplication is also referred to as butterfly method




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths
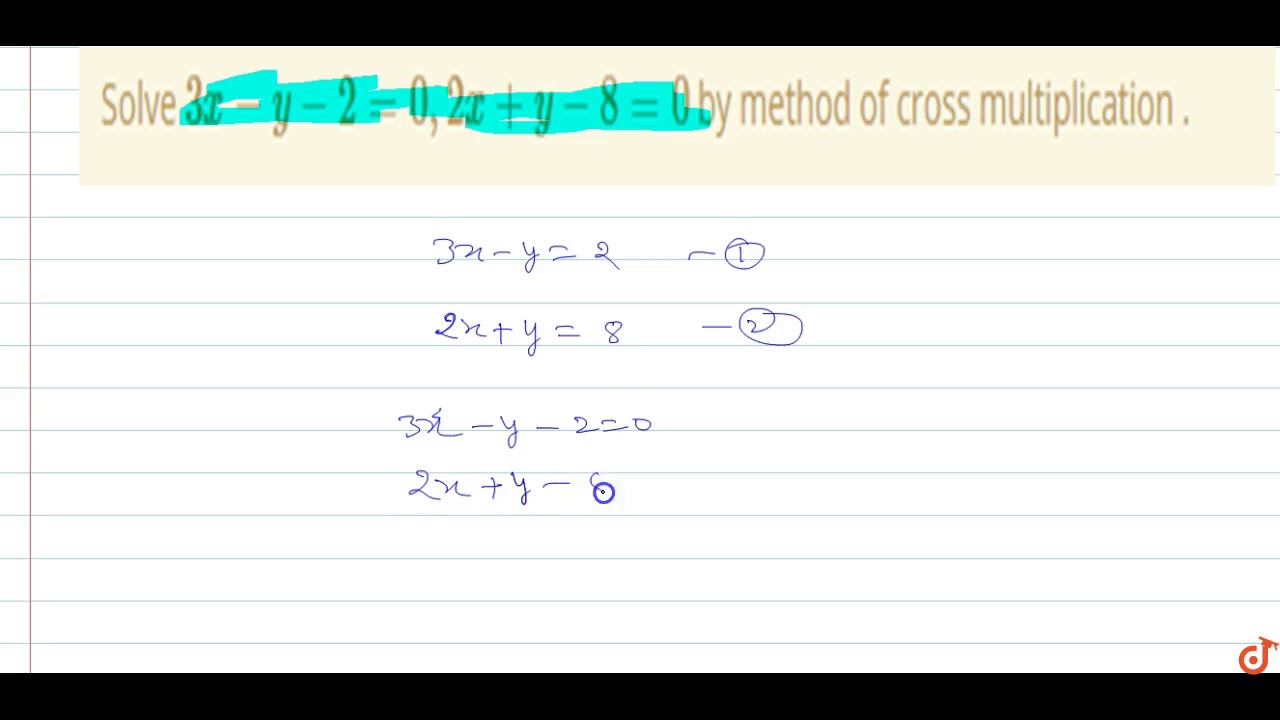



Solve 3x Y 2 0 2x Y 8 0 By Method Of Cross Multiplication Youtube




Based On Cross Multiplication Method Solve The Following Pairs Of Equations By Cross Multiplication Rule X2 Y3 4 0 X2 5y3 12 0 Then X Y Is Equal To



Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community
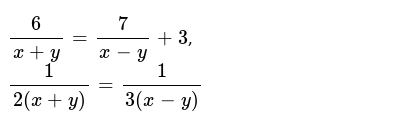



6 X Y 7 X Y 3 1 2 X Y 1 3 X Y



How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora




Ncert Class 10 Chapter 3 Pair Of Linear Equations In Two Variables




Chapter 3 Pairs Of Linear Equations In Two Variables Ncert Solutions For Class 9 Mathematics Maharashtra Topperlearning



Solving Systems Of Equations




Algebraic Elimination Method Class 10 Ncert Solutions Suresolv




X Y 3 X 3 Y 2 6 By Cross Multiplication Method Brainly In
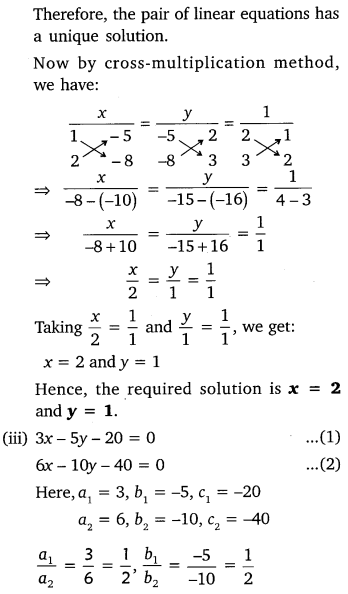



G 1 Coaching Class 3rd Chapter Pair Of Linear Equation In Two Variable



Systems Of Linear Equations



Solve The System Of Equations By Using The Method Of Cross Multiplication X 6 Y 15 4 X 3 Y 12 19 4 Sarthaks Econnect Largest Online Education Community




3 Systems Of Linear Equations




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples




Solve The Following System Of Equations By Using The Method Of
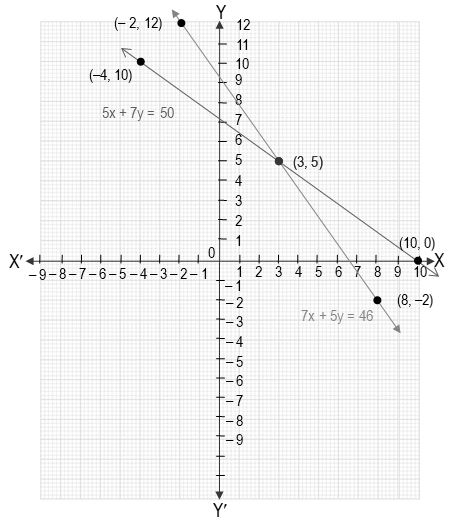



Pair Of Linear Equations In Two Variables



If 2x 3y 17 And 3x 5y 27 What Are X And Y Quora




Under The Surface Z Xy And Above The Triangle With Vertices 1 1 4 1 And 1 2 Homework Help And Answers Slader




X 2
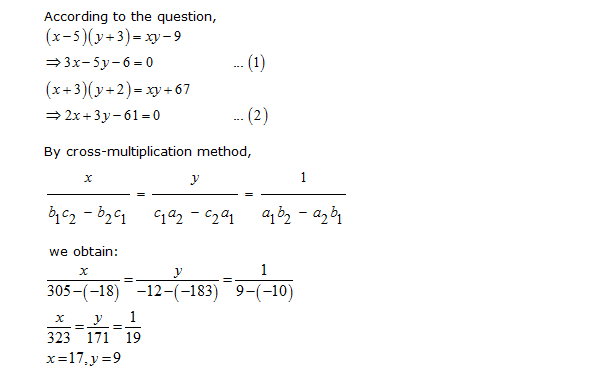



Chapter 3 Pairs Of Linear Equations In Two Variables Ncert Solutions For Class 10 Mathematics Cbse Topperlearning




Simplify Reduce Fractions With Step By Step Math Problem Solver




2 X 2 3y 1 6 And 3 X 2 Y 0 Problem Set 1 Q6 1 Of Linear Equation In Two Variables Youtube




Solve The Following System Of Equations By Method Of Cross Mult



Q Tbn And9gcrvxqxwilzvfrimds45eaf0inigyjgztv5jwx 4d0vooqeofoyk Usqp Cau




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4



Www Sfdr Cisd Org Media 7739 Drfs Algebra 1 Pdf




Solve By Reducing Them To A Pair Of Linear Equations 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Youtube




G 1 Coaching Class 3rd Chapter Pair Of Linear Equation In Two Variable




Updated Ncert Class 10 Math Pair Of Linear Equations In Two Variables Solution




Ex 3 5 1 Which Pair Has Unique No Solution Or Infinitely



How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora
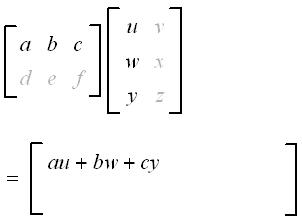



4 Multiplication Of Matrices




X 6 Y 15 4 X 3 Y 12 19 4 Solve Using Cross Multiplication Method Brainly In




X 6 Y 15 4 X 3 Y 12 19 4 Solve Using Cross Multiplication Method Brainly In



Www Sfdr Cisd Org Media 7739 Drfs Algebra 1 Pdf



Sehschool Files Wordpress Com 07 10th Algebra Lesson 1 Pdf



Solve The System Of Equations By Using The Method Of Cross Multiplication X 6 Y 15 4 0 X 3 Y 12 19 4 0 Sarthaks Econnect Largest Online Education Community




Systems Of Equations With Substitution 2y X 7 X Y 4 Video Khan Academy




Please Help Plz Help I Will Mark As Brilliantsolve By Cross Multiplication Method1 X 2y 1 0 And 2x Brainly In




5 X Y 2 X Y 1 And 15 X Y 7 X Y 10 Solve Equation By Cross Multiplication Method




Ex 3 5 3 Solve By Substitution And Cross Multiplication




Solve 2 X 2 3y 1 6 And 3 X 2 Y 0 And Hence Find A For




X Y 3 X 3 Y 2 6 Youtube




Solve 2 X 2 3y 1 6 And 3 X 2 Y 0 And Hence Find A For




5 Ways To Solve For X Wikihow
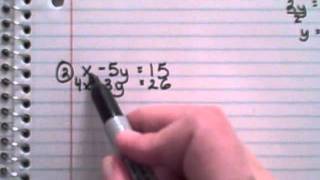



Linear Systems With Multiplication Algebra Socratic




Solve The Following Equation Using Cross Multiplication Method X 2 3 3x 5 6 5x 7 18



1




5 Ways To Solve For X Wikihow
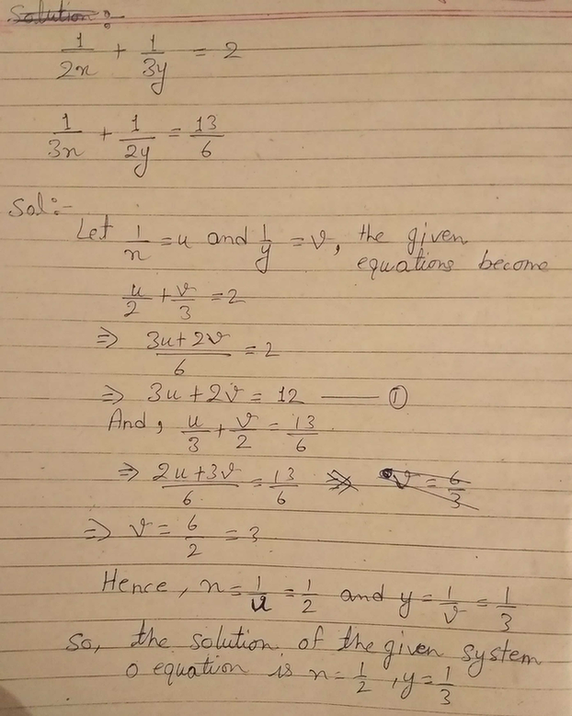



Exercise 3 5 1 Solve The Following Pairs Of Equations By Re Scholr




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4



1




Solve The Following System Of Equations By Method Of Substitutio
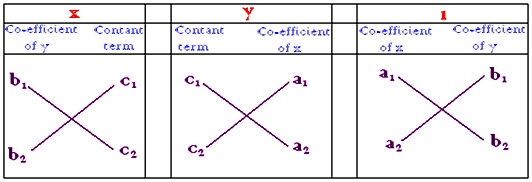



Cross Multiplication Method Formula For Cross Multiplication Linear Equations



Solve 5 X 1 1 Y 2 2 And 6 X 1 3 Y 2 1 Studyrankersonline




G 1 Coaching Class 3rd Chapter Pair Of Linear Equation In Two Variable




Selected Answers New Lexington City Schools
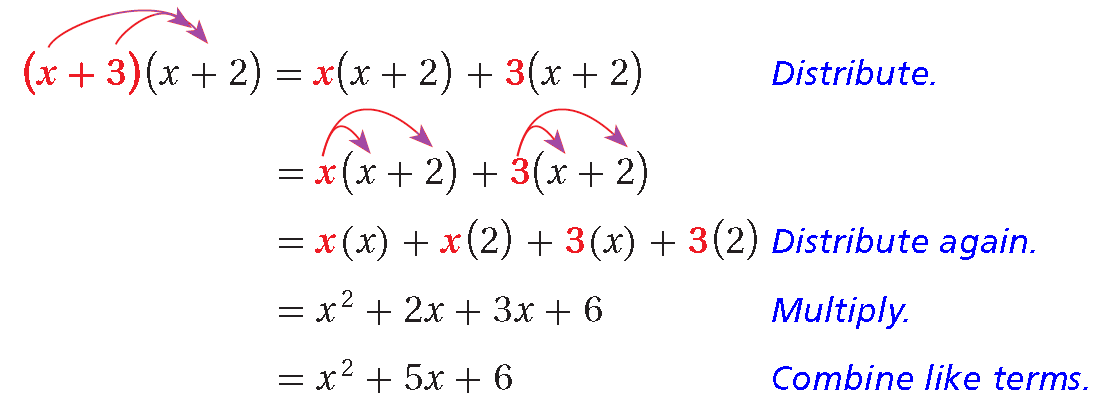



Multiplying Polynomials




Solve The Following System Of Equations By Method Of Cross Mult



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community




S4 Solve The Equation Using C See How To Solve It At Qanda
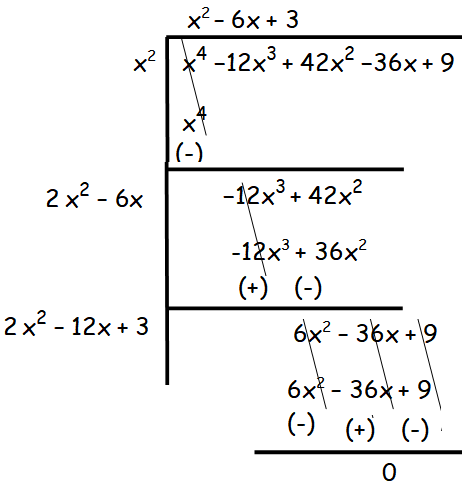



Finding The Square Root Of A Polynomial By Long Division Method



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora




Ex 3 5 3 Solve By Substitution And Cross Multiplication




S4 Solve The Equation Using C See How To Solve It At Qanda




3 Systems Of Linear Equations



S3 Ap South 1 Amazonaws Com 360degreedoc Institutes Caj 1 Lms Online Learning Pdf




Rational Equations Section Ppt Video Online Download




X 2y 1 0 2x 3y 12 0 Novocom Top




Solving Linear Equations By Cross Multiplication Method X 2y 2 X 3y 7 Brainly In




How To Solve Equations With Three Variables By Cross Multiplication Method Quora



Www Sfdr Cisd Org Media 7739 Drfs Algebra 1 Pdf
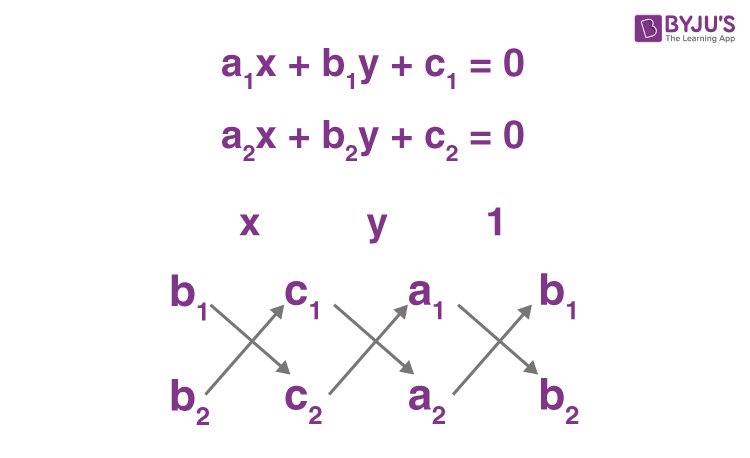



Cross Multiplication Method For Pair Of Linear Equations In Two Variables
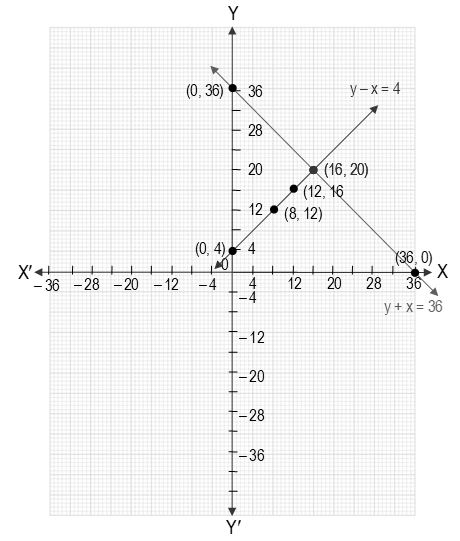



Pair Of Linear Equations In Two Variables




Solve The System Of Eq 2x 3y 17 3x 2y 6 By Method Of Cross Multiplication Brainly In




Solve The System Of Equations 2x 3y 17 3x 2y 6 By The Meth Scholr



No comments:
Post a Comment